Diffraction as a physical limitation

You are here: Nature Science Photography – Visual acuity – The resolving power of the visual system

Resolution refers to the degree to which the visual system rasters a scene. It corresponds to the packing density of the photoreceptors, which is greatest in the fovea centralis (see „The arrangement of photoreceptors on the retina“). We can say that the high resolving power in the fovea allows us to capture as many edges as possible with precision.

Our impression of the sharpness of a natural scene or a photograph is greater the more details we perceive. The resolving power of our visual system determines how much detail we perceive. We can relate this to different perceptual performances. We can ascertain the required minimum distance between two objects to perceive them as distinct. This is called resolution acuity. We can ascertain the minimum size of an object to maintain its recognition. This is called detection acuity. We can identify the smallest object size that is still perceptible. This is called minimum detectable acuity. And we can determine the smallest perceptible offset between two lines. This is then called hyper acuity or Vernier acuity. For our photographically oriented observation, the resolution acuity is relevant. It depends on several factors that add up to a measure that an image need not exceed to make a sharp impression. We will examine these factors in detail in the upcoming sections.

Light waves normally travel in a straight line through space. When light waves encounter or pass very close to an obstacle, defined as within a few wavelengths, they deflect from their normal straight path. This process is called diffraction. It is an unavoidable physical effect and independent of the quality of the optics. The smaller the aperture, the greater the image’s impairment by diffraction.

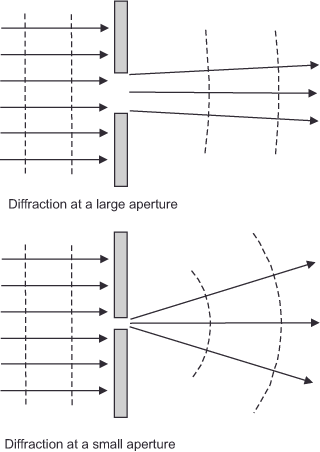
Due to this dispersion in different directions, the light waves then no longer all cover the same distance but partly leave their original direction of oscillation. This causes them to overlap and complement each other at one point or to completely or partially cancel each other out at another. This superposition (interference) produces a diffraction pattern that has the highest intensity where the waves add and the lowest where they cancel. If we were to measure the intensity at each position of a straight line, the result would be a band similar to that shown in

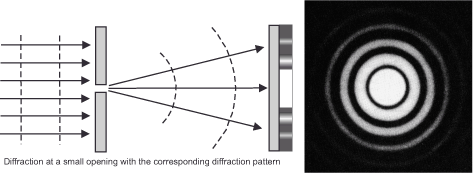
A perfectly round and therefore ideal aperture would produce a diffraction pattern called Airy disk after its discoverer, the British astronomer Sir George Biddell Airy (1835-1892). Transferred to a more practical case, we can imagine the diffraction as in a water hose. If there is enough pressure, the water exits the hose as a nearly circular jet. However, if we slightly compress the free opening with our fingers, the jet separates into a relatively wide fan.

Every optical device, including our eye, has an aperture limit because we cannot construct infinitely large optics. This limitation can be attributed to either the outer diameter or the size of a built-in aperture. This bottleneck deflects the light, preventing the optics from imaging a distant point source of light, even after eliminating all other aberrations. Instead, depending on the aperture size, the image turns out more or less blurred, and it reflects the general so-called Fraunhofer diffraction pattern in the focal plane. Often, this effect is negligible, yet it fundamentally hinders the capture of intricate details, thereby limiting image magnification beyond a specific threshold.

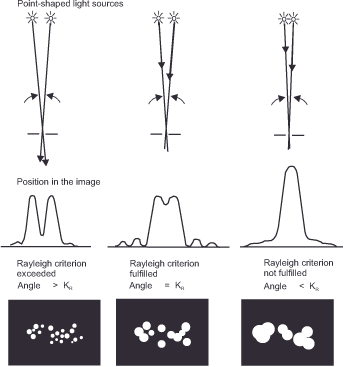
To describe the resolving power of an optical system, we use the Rayleigh criterion (C_R) named after its discoverer, John William Strutt (1842-1919), the third Lord Rayleigh. It states that two light points are considered to be resolved if the main maximum of the first does not fall below the first minimum of the second.

Maximum and minimum of the light sources must therefore be separated by a distance that is proportional to the quotient of light wavelength and aperture diameter. Thus, it is clear that a larger aperture can also resolve finer details. This relationship is expressed by the formula for a round aperture:

Formula 1

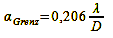
α Grenz = Resolution in radian dimension
λ = Light wavelength
D = Aperture diameter

For the resolving power of our eyes, the Rayleigh criterion also applies as a basic benchmark, and with the formula just introduced, we can calculate the theoretically maximum achievable resolving power. For this purpose, we assume a pupil diameter for the fully light-adapted eye of D = 3 mm on average and the wavelength λ= 550 nm, for which the receptor apparatus of the eye is most sensitive.

Calculation 1

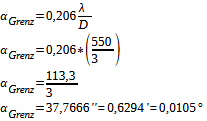
Theoretically, then, in daylight, we can distinguish two points that are just 0.6294 arcminutes apart. In other words, the two points must be 1 mm apart for us to perceive them as separate from a distance of 57 cm.

The larger the f-number, the larger the diffraction or Airy disk. The question that now arises is: „At what point does diffraction become a limiting factor for detail reproduction, i.e., resolution?“ To answer this, we must first consider at what point humans perceive the diffraction discs as separate points. Lord Rayleigh conducted and published this investigation in 1879. The investigation reveals that for the eye to perceive two Airy disks as separated, the intensity of the area between them must have dropped to 81 % of their maximum intensity. This is exactly the case when the maxima of the diffraction discs have a distance equal to the radius of one disc.

Next The arrangement of photoreceptors on the retina

Main Visual acuity

Previous Positioning – What is visual sharpness?

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!