The focus – true geometric sharpness only exists in one plane

You are here: Nature Science Photography – Visual acuity – Image sharpness I

To capture a visually sharp image, we must first ensure geometric sharpness. To put it another way, we must ensure that a point appears as a point. To understand why this is not the case by itself, let’s dive into the optical basics of image formation for a moment. Figure 23 (Simplified imaging system)shows a basic imaging system: An object to be photographed, a lens reduced to a single optical component, and the film lying in its own plane.

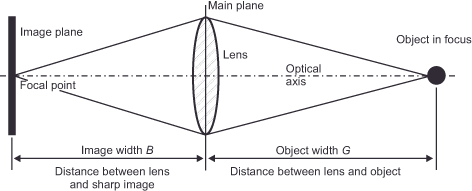
The motif reflects light in all directions, but for our consideration of the image formation, only that part is relevant, which falls on the lens. It is represented by the lines running from the object point to the outer edges of the lens. Simultaneously, these lines represent the outer boundary of the cone of rays that emanate from each small part of the subject point. Each of these cones has its apex at the object and its base at the center of the lens. It then focuses on the film, creating a second ray cone with its base at the lens center. Its vertex is located where the sharp image is formed. This establishes a mathematical relationship between a) the distance from the lens’s center to the sharp image (image distance B), b) the distance from the lens’s center to the photographed object (object distance G), and c) the focal length (f) of the lens. It reads: The reciprocal of the image width plus the reciprocal of the object width equals the reciprocal of the focal length, or expressed mathematically:

Formula 5 – The lens formula

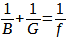
B = Image distances
G = Object distance
f = Focal length of the lens

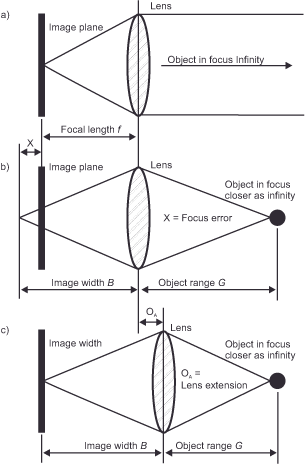
The focal length is defined as the image distance at which an object located at infinity, i.e., very far away, e.g., a mountain on the horizon, a building on the other side of the city, or the moon in the sky, is sharply imaged. The film plane lies at exactly this image distance. It follows that the sharp image of an object closer than infinity is located behind the film plane. This is illustrated in figure 24 (focus infinity and closer). It shows in a) the constellation in which an object located at infinity is imaged in the film plane, b) shows the constellation in which the sharp image of an object located closer than infinity comes to lie behind the film plane at the same focus setting. If we want to take a sharp image of this closer-than-infinity object, we must therefore move the lens far enough away from the film plane so that the sharp image comes to rest exactly on it. This process, the alignment of the focal point and the image plane, is called focusing, and you have probably noticed that the length of most lenses increases the shorter you set the distance. Figure 24 c shows how the image of this closer object is brought into alignment with the film plane by moving the lens away from it.

In geometrical optics, the focus is the focal point of an optical lens or concave mirror. This is the place where the light rays incident parallel to the optical axis converge.

For our focus-oriented observation, this means that a lens can only ever really focus on the focal plane and that all objects in front of and behind this plane are more or less out of focus. In other words, the lens will only image the focused point as a point. Points that lie in front of or behind it are imaged as more or less large slices because their sharp image lies in front of or behind the film plane. The difference between the film plane and the sharp image is called the focus error (X), and the slice is called the circle of confusion (Z). It is the traditional measure of sharpness. We must clarify that „sharp“ always refers to the limits set by diffraction. In the section about „Diffraction“ we have learned why this is so.

To simplify the matter, I declare the lens systems of the objectives in question to be a single „thin lens“. The advantage is that we can measure distances in front of and behind the lens from one plane. Actual lenses consist of several individual elements, collectively called a „thick lens“. They usually have two main planes at which the rays incident parallel to the optical axis are refracted.

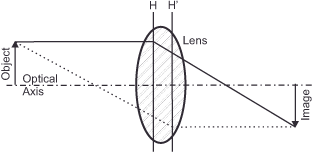
So, if we are very precise, the distances in front of the lens (e.g. the object distance) and those behind the lens (e.g. the image distance) must be determined from the front and rear principal planes, respectively. We can disregard them with a clear conscience, as a) obtaining the relevant measurements for real lenses is difficult or even impossible, and b) the distances are so small that they are hardly noticeable in normal pictorial photography.

Next Circle of confusion and depth of field – Perceived sharpness extends over more than one plane

Main Visual acuity

Previous What the visual system does with object edges

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!