RGB, CMYK – Description of impressions in device-dependent reference systems

You are here: Nature Science Photography – Lightness and color – The reproduction of lightness and color

Within the additive and subtractive color models, we can describe a certain color based on the proportions of the respective primary colors. Green, for example, can be defined as 0 % red 100 % green 0 % blue. Cyan would correspond to 100 % cyan 0% magenta 0 % yellow and so on. Graphically, we can therefore represent both models as three-dimensional coordinate systems: as cubes, on whose main axes (width, height, depth) the saturation values of the three primary colors are plotted. In the additive model (figure 33), we find black at the intersection of all three straight lines (the coordinate origin in the lower back corner), which occurs when there are zero light components that can mix. At the axis pointing to the right we find blue, at the axis pointing to the left we find green and at the vertical axis we find red. Conversely, in the subtractive model (figure 34), at the intersection of the three straight lines (the coordinate origin in the upper front corner), we find white, which is created when the mixing fraction of all three colors is zero, i.e., no fraction of the total spectrum is absorbed. Magenta is located on the axis pointing to the right, yellow on the axis pointing to the left and cyan on the vertical axis.

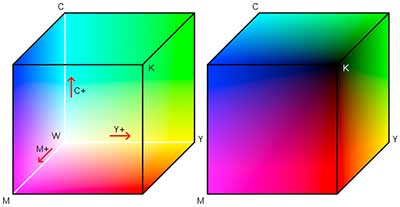
So much for the theory. In practice, it looks less clear, because depending on the output device, the primary colors involved (and therefore also the mixed colors) can be of one kind or another. The additive primary colors red, green and blue, for example, are theoretically exactly determined by the wavelengths of their spectral counterparts (red 650 nm, green 530 nm, blue 440 nm), but in practice they are not generated by splitting the spectrum with a prism and therefore cannot be reproduced exactly. Put two computer monitors, on which a computer outputs the same image, next to each other and compare the colors. They will almost certainly differ in some areas. Each manufacturer does its own thing, and manufacturing tolerances mean that the basic colors will be slightly different for each device. The situation is similar for the subtractive dyes used in films, photographic papers, printing presses and desktop printers, and therefore also for their mixed colors. Today, it is technically impossible to produce these dyes in a way that absorbs 100% of one spectral range and transmits 100% of the other. In practice, a part of the spectrum that is not actually wanted always slips through, and the combination of such dyes deviates from our simple rules. Cyan, magenta, and yellow therefore do not result in black but rather a dirty brown. The printing industry developed the CMYK model, adding black as a fourth color, to make everything workable. The K in CMYK stands for the concept of the key color, which is not used for coloring but only for darkening the colors, making it possible to print pure black. The second necessary consequence is that the statement Yellow + Magenta = Red cannot be practically true. The mixture will produce a red color, but not the basic red color in the additive model.

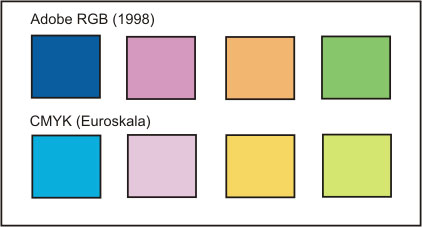
Each type of monitor, each type of printer and each type of film, in short, all output devices and media must therefore, for the technical reasons mentioned, work within their color models in color spaces of their own size. This has far-reaching consequences. Let’s go back to figure 33 (RGB cube) and figure 34 (CMY cube). The total number of mixable colors (the representable color space) decreases by exactly this amount if the primary colors, as is almost always the case in practice, are not as saturated as the theoretically ideal colors and do not lie as far inside or outside the coordinate system as the latter. A certain color space will therefore contain colors that cannot be represented in a comparatively smaller one but can only be approximated. Figure 35 illustrates this relationship. Furthermore, the color values given in percent saturation are no longer transferable 1:1 between these spaces. A green, for which the definition given at the beginning 0 % red 100 % green 0 % blue applies, will necessarily look different if it is converted into a color space with deviating primary colors.

For these reasons, the device-dependent color spaces are suitable for the relative, but not the absolute description of color values. In order to be able to compare color values in general and the corresponding reproduction properties of our image carriers in particular, we need a device-independent mathematical model that includes all colors.

A color model specifies the representation of colors and the generation of their mixtures. On the other hand, a color space represents a specific expression of a color model associated with a device.

Next CIE-Lab – Description of impressions in device-independent reference systems

Main Lightness and Color

Previous The technical generation and description of brightness and color impressions

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!