Geometry and calculation of the depth of field

You are here: Nature Science Photography – Visual acuity – Image sharpness I

The introductory section has demonstrated that a discrepancy between the film plane and the sharp image, known as the focus error X, results in a blurred image at an image point, commonly referred to as a circle of confusion Z. At this point, it is now useful to make a distinction between the circle of confusion Z, which exists under certain conditions, and the maximum allowable circle of confusion z on the one hand, and the focus error X, which also exists under certain conditions, and the maximum allowable focus error x on the other hand. We have previously determined the visually based maximum permissible size of the circle of confusion. Now we are interested in how large the focus error may be at its maximum without the blur becoming perceptible in the image. We first consider and determine the depth of field on the image side, also known as the depth of focus, before moving on to the practically more relevant depth of field on the subject side.

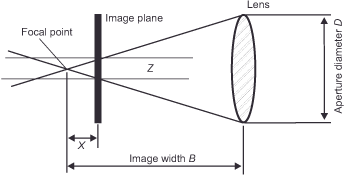
Figure 26 (Circle of confusion and focus error) illustrates the relationship between circle of confusion Z, focus error X, image width B, and effective aperture diameter D, which is expressed mathematically in the following formula:

Formula 7

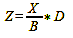
If we assume that the image distance is approximately equal to the focal length (which is usually the case as soon as the lens-to-object distance is at least ten times the lens focal length), we can simplify the formula:

Formula 8

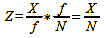
From the simplification, we can read off that a) the focal length f plays no role for the size of the circle of confusion because it shortens away, b) its diameter is directly proportional to the focus error X and c) inversely proportional to the f-number N.

We convert formula 3 to obtain the maximum permissible focus error x:

Formula 9

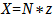
The maximum permissible focus error x, which is the same on both sides of the image plane (the distance between the image plane and the point Bv or the image plane and the point Bh in the figure 26 (Circle of confusion and focus error) is therefore equal to the product of the maximum permissible circle of confusion z and the set aperture number N. For example, let’s consider aperture 4 and z=0.03 mm:

Calculation 9

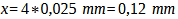
To infer the extent of the image-side depth of field, we need to know the different image widths. This refers to the distances between the main plane and the image plane B, or between the main plane and the front and rear limits of the image-side depth of field Bv and Bh. The lens formula (formula 5 in „The focus – true geometric sharpness only exists in one plane“) is rearranged to determine these image widths:

Formula 10

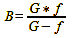
For a situation in which the lens with focal length f = 50 mm is set to a distance G = 2000 mm (measured from its front side), the result is as follows:

Calculation 10

The distance to Bv in front of the film plane is equal to B-x, that to Bh behind the film plane is equal to B+x:

Calculation 11

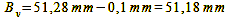
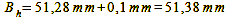
Thus we have the values for the image-side depth of field of the combination f = 50 mm, f/4, z = 0.025 mm, G = 2000 mm. In reality, however, we are interested in the extent of the sharp area on the object side. – After all, we want to know what part of our subject will appear acceptably sharp in the image. To determine it, we project the points Bv and Bh onto this other side. These are the points Sv and Sh
in figure 27 (object-side depth of field). Formula 5 (the lens formula in „The focus – true geometric sharpness only exists in one plane“) gives us the possibility to do this after another conversion because it puts image width B, object width G and focal length f in relation to each other:

Formula 11

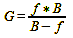
For our exemplary case it then looks like this:

Calculation 12a, 12b, 12c

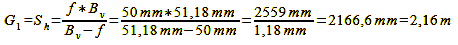
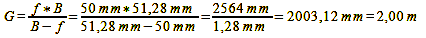
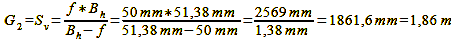
While the result for G does not precisely match our underlying object distance of 2000 mm, it remains accurate enough, considering that this is an approximation formula. Upon completing these computations, it’s important to acknowledge that the distribution of the object-side depth of field no longer exhibits the same level of symmetry as the permissible focus error/image-side depth of field.

Calculation 13a, 13b

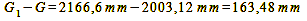
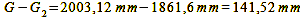
This non-symmetrical division, caused by the non-linearity inherent in formula 10, will be encountered several times in the course of our further consideration of the properties of depth of field. Now, it is admittedly rather laborious and complicated to calculate the depth of field in this manner, which is necessary for understanding the fundamental relationships. For this reason we want to resolve the lens formula (formula 5 in „The focus – true geometric sharpness only exists in one plane“) directly for object width G, focal length f and permissible focus error x:

Formula 12

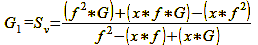
Formula 13

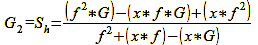
Let’s briefly insert the values to check if everything is correct:

Calculation 14

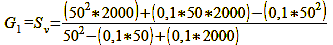
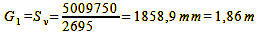
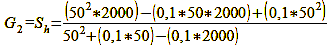
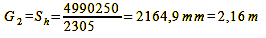
Wonderful, everything corresponds perfectly with the numbers determined above! The total depth of field is obtained by subtracting Sv from Sh or by calculating formula 13:

Formula 14

Naturally, this walk becomes excessively strenuous over time. Therefore, I recommend one of the numerous depth of field calculators available on the web. But I want to point out right away that the results are only approximate: The calculation is not exact. Every lens has optical errors; films produce halos; the exact circle of confusion diameter depends on the viewing distance and the resolving power of the eye. All in all, however, we are still dealing with very good approximations. In the following three sections, we will vary the factors aperture, shooting distance, and focal length combined in the formulas to see how this affects the depth of field.

List of formula abbreviations and acronyms

f	Focal lenght of the lens
N...	f-stop number
D	Aperture diameter
A	Distance lens to film
Z	Circle of confusion
z	Maximum permissible circle of confusion
X	Focus error
x	Maximum permissible focus error
G	Subject distance
B	Image distance, distance between main plane and sharp image
Bv	Front limit of the focal depth
Bh	Rear limit of the focal depth
S	Total depth of field
Sv	Front limit of depth of field
Sh	Rear limit of depth of field
H	Hyperfocal distance
F	Format factor
OA	Lens extract
Fd	Focus distance

Next Depth of field and aperture

Main Visual acuity

Previous Circle of confusion and depth of field – Perceived sharpness extends over more than one plane

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!