Electronic image carriers – analog and digital

Now we know that a CCD or CMOS chip produces an analog electrical signal as its output variable, which describes the light intensity strength. As a result, the chip is an analog image carrier at its core. The difference between digital and analog photography is the conversion process that takes place after the analog sensor captures the image. This conversion resulted in all the advantages and disadvantages of digital photography. To understand what happens, let’s first take a quick look at what digital data is and how we should think of bits and bytes. The easiest way to understand this is to compare it to something we are familiar with: digits. A digit is a single position that can take values between 0 and 9, and digits are usually grouped together to express larger numbers. For example, the number 2,354 has four digits, and it is clear that the 4 fills the ones digit, the 5 fills the tens digit, the 3 fills the hundreds digit, and the 2 fills the thousands digit. You could also express the relationship as follows to be completely correct:

(2*1000) + (3*100) + (5*10) + (4*1) = 2000 + 300 + 50 + 4

We get an identical different expression when we work with the power of ten:

(2*10³) + (3*10²) + (5*10¹) + (4*10⁰) = 2000 + 300 + 50 + 4

From this, we can see that each digit is a placeholder for the next higher power of ten, starting with the first digit with 10⁰. So far, so good. We work with decimal numbers every day. The nice thing about number systems is that nobody forces you to have ten different values in one digit. Our ten-digit system probably evolved because we have ten fingers. But if evolution had equipped us with only eight such tactile devices, we probably would have come up with an eight-number system. In principle, you can work with a whatever-number-system, it’s just a matter of arrangement. Computers, because of their underlying technology (they know only two states: current flowing or current not flowing), work with the two-number system, which we also know as the binary system. So they use binary digits and numbers instead of decimal ones and the word bit is just a summary of the expression binary digit or binary number. Where decimal numbers have ten possible values between 0 and 9, bits have only two, 0 and 1, from which they build a number like 1011. We determine the value of this 1011 in the same way as we did for the 2354, but we use a power of two instead of ten:

(1*2³) + (0*2²) + (1*2¹) + (1*2⁰) = 8 + 0 + 2 + 1 = 11

In binary, each bit holds the value of an increasing power of two and this makes binary counting quite easy. From 0 to 20, this looks like this in decimal and binary:

0 = 0
1 = 1
2 = 10
3 = 11
4 = 100
5 = 101
6 = 110
7 = 111
8 = 1000
9 = 1001
10 = 1010
11 = 1011
12 = 1100
13 = 1101
14 = 1110
15 = 1111
16 = 10000
17 = 10001
18 = 10010
19 = 10011
20 = 10100

In this sequence for the decimal system and the binary system, 0 and 1 are identical. Only at 2 the transition takes place for the first time. If 1 is bit 1 and 1 is added to it, the bit becomes 0 and the following 1. At the transition from 15 to 16, this effect changes from four to five digits and turns the 1111 into the 10000.

Bits are relatively seldom seen alone in the computer. Typically, they manifest in groups of eight, known as bytes. Why does a byte consist of eight bits? Good question, but why do 12 eggs make a dozen? – The 8 bit byte is simply a convention that everyone has agreed upon. With a byte of eight bits, 256 values between 0 and 255 can be represented:

  0 = 00000000
  1 = 00000001
  2 = 00000010
....
254 = 11111110
255 = 11111111

Now we have enough basic knowledge to return to the practical application. The sensor cells on the chip initially provide us with analog electrical signals. At low brightness, a small current flows. At high brightness, a large current flows. In between, there is a virtually infinite number of gradations. Figure 22 (Bit width & brightness signal) illustrates this for a simple grayscale transition and assumes, as in real life, that the current intensity is linear to the brightness.

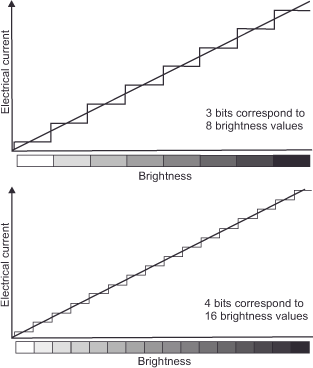
The component in the camera responsible for converting this analog signal to digital data is the analog-to-digital converter (A/D converter). It works as follows: Let’s think of each photocell as a bucket, and the incident light photons as raindrops. When the drops fall into the bucket, water accumulates in it (in reality, of course, it is electric current). More water is in some buckets than others depending on subject brightness. The A/D converter now determines the depth of water in each bucket, which is an analog quantity, and converts it to the desired binary form. Since the computer, as we learned above, can only distinguish between „current flows“ and „current does not flow“ and therefore works in the binary two number system, it reproduces the linear curve in the form of a staircase. How close the steps of the staircase are to each other, i.e., how fine the gradations are and how precisely the actually infinite number of tonal value gradations of the curve can be reproduced accordingly, depends on the number of bits with which the converter works internally, which we also call bit width or color depth. A 3-bit A/D converter generates 23 = 8 gradations, a 4-bit A/D converter 24 = 16 gradations, an 8-bit A/D converter 28 = 256 gradations, a 12-bit A/D converter 212 = 4096 gradations, a 16-bit A/D converter 216 = 65 536 gradations, and so on. In practice, we encounter A/D converters with 12-14 bits in the field of digital cameras. Since we work in the RGB color model and therefore have to deal with three individual color channels, they are referred to as 24-bit A/D converters or 36- or 48-bit A/D converters. The A/D converter’s bit width or color depth increases the number of brightness gradations in each of the three color channels, thereby improving the accuracy of the analog input signal reproduction. Only after this step is the data processed further by the camera’s microprocessor. And because the microprocessor only works with binary digital values, data conversion is necessary in the first place.

Next Electronic image carriers – Digital weaknesses

Main Image creation, Depth and Size

Previous Electronic image carriers – CCD and CMOS

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!