Depth of field and image format

You are here: Nature Science Photography – Visual acuity – Image sharpness I

It is often written that point-and-shoot digital cameras with small image sensors produce images with greater depth of field than those with larger sensors or cameras for 35 mm, medium or large format film. One might infer from this statement that the large depth of field is a property inherent in the small format size or the digital way of producing images. But both are wrong, and the described context is unduly shortened. For this reason, if you missed the factor „image format“ in the preceding section on the factors influencing the depth of field, it wasn’t due to inattention or a mistake. The format only exerts an indirect influence on the depth of field. Three common formats demonstrate this effect: We have the 1/2.5″ format (5.8×4.3 mm, image diagonal 7.22 mm) on the small side, the 35mm (24×36 mm, image diagonal 43.3 mm) in the middle, and the „small large format“ (4×5″, 100×130 mm, image diagonal 164 mm) at the wide end. To ensure the image results are truly comparable, we must enlarge them to the same final format and adjust the maximum permissible circle of confusion diameter z to match the corresponding enlargement factor. If we assume the 20×30 cm format, z is 0.018 mm for the small digital format or 0.03 mm in 35 mm and 0.1 mm in large format. Furthermore, it is crucial to ensure that all images display the same image angle.

The image angle α is the angle between the image rays in figure 32 (image angle). It determines which space the lens captures and how large it images the objects. Its size depends on the focal length, the distance setting and the size of the recording medium. Depending on whether its specification refers to the width, the height or the diagonal, we distinguish the horizontal angle of view, the vertical angle of view or the diagonal angle of view. If there is no precise definition, the value usually refers to the diagonal angle of view.

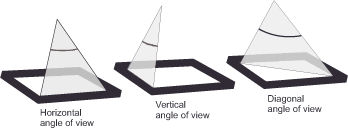
To calculate the angle of view α, we use formula 20:

Formula 20

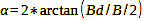
With the image distance B (distance between image-side main plane and sharp image), formula 20 contains a normally unknown quantity, which we must replace by a known one. In many books and on most websites on the subject, this is done in the way Image width = Focal length and leads to formula 21:

Formula 21

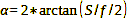
This is acceptable, but the formula and B=f condition are only correct if the focus is at infinity. For this and all other cases, it is correct to replace the image distance by the expression B=f*G/(G-f), which also results from the lens equation. Then we obtain formula 22:

Formula 22

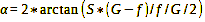
To conclude this mathematical excursion, let us note that the angle of view is determined by the focal length, the image format and the focus distance. Now, let’s return to the beginning of our format comparison and calculate the angle of view for the 35 mm format, which has a standard focal length of 50 mm and an image diagonal of 43.3 mm.

Calculation 23

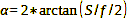
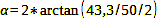
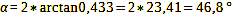
In order to cover the same angle of view with the other two shooting formats, you now have to do what? – Exactly: Adjust the focal length. We use formula 23 to calculate the value to which it must be changed in each case:

Formula 23

For the 1/2.5″ digital sensor with its image diagonal of 7.22 mm, it follows:

Calculation 24

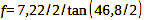
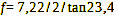
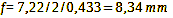
And in the case of the 4×5″ large format with the image diagonal of 164 mm, this is how things look:

Calculation 25

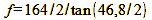
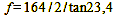
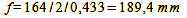
Alternatively, we can calculate the focal length required in each case by dividing or multiplying the values by the format factor F. The format factor indicates the length ratio between the diagonals of the image formats. For the ratio between 35 mm format and 1/2.5″ sensor, it is 43.3/7.22 = 6 and 50 mm focal length/6 = 8.33 mm. In the case of the comparison between 35 mm format and 4×5″, the format factor is 164/43.3 = 3.79 and 50 mm*3.79 = 189.5 mm.

For the same angle of view and aperture, the depth of field changes proportionally to the format factor.

Up to here, we have already gone a long mental way. At its end, we can see that three images taken a) in the small digital format 1/2.5″, b) in the 35mm format 24×36 mm and c) in the 4×5″ large format with identical aperture and format-equivalent circle of confusion diameter and enlarged to the same final format show different depths of field because different focal lengths are required to record the same image section or image angle. The focal length directly influences the sharp area of the image. As we noted in the corresponding section („Depth of field and focal length„), the depth of field increases as the focal length decreases. Qualitatively, for a window between macro range (C > f) and hyperfocal distance (f2/N*z), we can say that the depth of field is inversely proportional to the square of the focal length. Halving them doubles the depth of field. If we halve the format and produce an identically large print with the same aperture and the same image angle but with an adjusted circle of confusion diameter, the depth of field of the image taken in the smaller format is doubled. In even simpler terms, the change in depth of field is directly proportional to the format factor. The image taken in the small digital format shows a depth of field six times greater than that taken at 35mm, and again, it is 3.79 times greater than in the 4×5“ format. But beware: as we noted at the very end of the section „Geometry and calculation of the depth of field„, generalizations of the kind given should be taken with a grain of salt. So also here. As soon as the object distance reaches the hyperfocal distance, the depth of field increases rapidly. As this happens first for the shorter focal length of the smaller format (where the hyperfocal distance is smallest), the depth of field ratio between the respective two formats also increases. In summary, the camera with a 1/2.5“ sensor and an 8 mm lens, near or directly at the hyperfocal distance, exhibits a depth of field more than six times greater than a 35 mm camera with a 50 mm lens. At these points, the ratio can double or triple this value because the far point of the depth of field shifts very quickly toward infinity.

However, you can easily offset this depth of field advantage by stopping down further in the larger format, taking into account the format factor. Assume that we set all lenses in our comparison to f/2.8. To achieve the same depth of field in 35 mm as in the small digital format, we would have to stop down to 2.8*6 = 16.8, i.e., f/16. Likewise, if we wanted to achieve the same depth of field in 4×5″ format as in 35 mm, we would have to stop down to 2.8*3.79 = 10.6 or f/11. Examining these figures closely reveals that the significant increase in depth of field in smaller digital formats also comes with a drawback. Because if they already deliver the same depth of field at f/2.8 as f/16 in 35 mm, this means that, depending on the focal length, it may not even be possible to stop up far enough to create the desired blur. And of course, the need to stop up and down has consequences when sharpness is limited by either aberration or diffraction (see „Circle of confusion and diffraction slice„). Anyway, it should now be clear where the term „digital camera equals large depth of field“ originates from!

Next Estimating the depth of field when taking a picture

Main Visual acuity

Previous Depth of field and focus point

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!