Depth of field and focal length

You are here: Nature Science Photography – Visual acuity – Image sharpness I

Again, we first use the data from the previously performed calculations 16 a and 16b. Their key data are thus f=50 mm, S=5000 mm, f/8, z=0.03 mm, Dv =3.39 m, Dh=9.53 m, S=6.14m. For calculations 19a and 19b it is f=100 mm, S=5000 mm, f/8, z=0,03 mm, Dv 5.67 m, Dh = 4,47 m, S = 1.2 m

So lengthening the focal length costs us depth of field, and shortening it gives us a larger acceptably sharp area. Again, we can explain this behavior mathematically: When we double the focal length, the numerators in Dv and Dh quadruple, but the denominators increase in a different proportion. The one in Dv triples, and the one in Dh approximately increases sevenfold. In sum, both fractions reduce in comparison to the shorter focal length, and the depth of field shrinks. And here again we find the already known non-linearity between the acceptably sharp area in front of the focus point and the one behind it. This is because Dv decreases less than Dh, and therefore the depth of field shifts more and more in favor of the closer area as the focal length increases. Of course, Table 4 provides a breakdown that illustrates this phenomenon across a wide range of focal lengths.

Focal length	Percentage of depth of field in front of the focus point	Percentage of depth of field behind the focus point
10 mm	70,2 %	29,8 %
20 mm	60,1 %	39,9 %
50 mm	54,0 %	46,0 %
100 mm	52,0 %	48,0 %
200 mm	51,0 %	49,0 %
400 mm	50,5 %	49,5 %

Again, the ray paths in figure 30 (focal length and depth of field) explain what is happening a bit better than the mathematics.

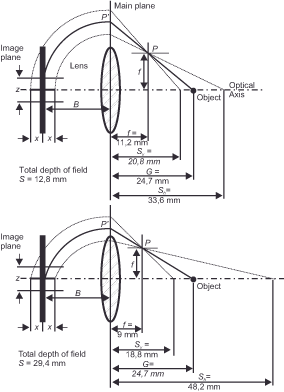
Therefore, in the calculations from the previous two sections, the depth of field also increased as the corresponding factor increased. However, when it comes to the focal length, the situation is reversed. Why? Two sections earlier, we learned that a) the effective aperture diameter is obtained according to the relation d = f/N (diameter = focal length/aperture number) and b) the depth of field increases when the aperture is decreased. Since long focal lengths have larger effective aperture diameters than short ones (d = 24mm/5.6 = 4.3 or d = 200mm/5.6 = 35.7), they must therefore inevitably have a shallower depth of field. Thus, mathematics confirms what we commonly know: Wide-angle lenses have a greater range of sharpness than telephoto lenses.

Focal length / f/stop	f/2,0	f/2,8	f/4,0	f/5,6	f/8,0	f/11	f/16	f/22
24 mm	∞	∞	∞	∞	∞	∞	∞	∞
50 mm	5,06 m	7,53 m	12,37 m	24,19 m	218,1 m	∞	∞	∞
100 mm	1,19 m	1,67 m	2,41 m	3,42 m	5,04 m	7,31 m	12,28 m	22,8 m
200 mm	0,29 m	0,41 m	0,60 m	0,82 m	1,18 m	1,63 m	2,38 m	3,32 m
400 mm	0,072 m	0,10 m	0,14 m	0,20 m	0,29 m	0,40 m	0,58 m	0,79 m

However, numerous print and web publications lead us to believe that magnification scale and aperture more closely influence depth of field than focal length. They support this claim with sample images and figures, demonstrating that, if the object’s image size remains constant, the total depth of field remains approximately the same regardless of focal length. Let’s get to the bottom of this assertion with Tables 6 and 7 below.

Scale of reproduction / Focal lenght	24 mm	50 mm	100 mm	200 mm	400 mm
1:2	0,00010 m	0,00010 m	0,00010 m	0,00010 m	0,00010 m
1:1	0,00034 m	0,00033 m	0,00033 m	0,00033 m	0,00033 m
1:10	0,0182 m	0,0185 m	0,0185 m	0,0185 m	0,0185 m
1:100	1,94 m	1,75 m	1,71 m	1,70 m	1,70 m
1:1000	∞	∞	571,22 m	204,19 m	175,39 m

Scale of reproduction / Focal lenght	24 mm	50 mm	100 mm	200 mm	400 mm
1:2	0,00039 m	0,00039 m	0,00039 m	0,00039 m	0,00039 m
1:1	0,00132 m	0,00132 m	0,00132 m	0,00132 m	0,00132 m
1:10	0,074 m	0,073 m	0,073 m	0,073 m	0,073 m
1:100	∞	11,81 m	7,48 m	6,85 m	6,71 m
1:1000	∞	∞	∞	∞	2069 m

These two tables demonstrate that the claim that the depth of field solely depends on magnification is only partially accurate for scales ranging from 1:2 to 1:10. For smaller scales, on the other hand, it is no longer valid, but the depth of field decreases with increasing focal length. Therefore, what we observe is simply an exception to the rule. The widespread misconception that the depth of field is independent of the focal length, as long as the magnification scale remains the same, may stem from the fact that this statement holds approximately true for frequently used focal lengths, such as portraits or still lifes. However, when it comes to landscape photographs, this assumption is significantly inaccurate. Often, landscape photographs lack a primary subject, which is why maintaining a constant magnification makes no sense. Changing the focal length and maintaining a constant magnification at a specific distance will inevitably alter the size of the more distant or closer parts of the subject.

If we look closely at the numbers, as Table 8 does for the particularly representative anomaly window, we can learn something else. Specifically, the percentage of distance decreases as the focal length increases, even when the total depth of field stays constant. This inversely proportional behavior causes the depth of field to appear small and the space to appear gathered, which explains why we either love or hate telephoto focal lengths.

Focal lenght f	Distance S	Near point D1	Far point D2	Depth of field S	Depth of field as a proportion of the distance in %
24 mm	26,4 cm	24,0 cm	29,33 cm	5,33 cm	20,2
50 mm	55,0 cm	52,48 cm	57,77 cm	5,29 cm	9,7
100 mm	110,0 cm	107,00 cm	113,00 cm	5,28 cm	4,8
200 mm	220,0 cm	217,00 cm	223,00 cm	5,28 cm	2,4
400 mm	440,0 cm	437,00 cm	443,00 cm	5,28 cm	1,2

At the very end of these three sections on the main factors influencing depth of field, you may wonder why I have left it at very general statements like „stopping down increases depth of field“ and not given you any clear announcements à la „reducing the aperture by one stop doubles the depth of field“. – Several publications on the subject follow this approach. In principle, the answer is clear based on the calculations: All these sweeping statements, such as „doubling the distance quadruples the depth of field“ or „halving the focal length quadruples the depth of field“, only apply to a narrow distance window. This window is not in the macro range, where the object distance must be several times greater than the focal length, nor is it close to the hyperfocal distance, which corresponds to f2/N*z, as discussed in the following section. There they correctly reflect the tendency of the change but quickly fall apart above and below it. The best example of this is the hyperfocal distance. As the focus distance approaches it, the depth of field increases quasi-exponentially. This happens much sooner with short focal lengths than with long ones, because the hyperfocal distance is smaller there. At the end of all descriptions, depth of field has a quantity derived from the formulas, and we must accept that striking „over-the-thumb rules“ cannot fully capture its inherent complexity. For this reason, almost everything you hear or read about depth of field is inaccurate under certain conditions, and the only qualitative statements that are nearly universally applicable are the ones I have used.

Next Depth of field and focus point

Main Visual acuity

Previous Depth of field and subject distance

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!