Building blocks of our size perception – The settlement of distance

You are here: Nature Science Photography – Image creation, Depth and Size – Size perception

Afterimages are a good example of the importance of distance perception in size construction. They occur when the photoreceptors of the retina are quasi-fatigued by a bright light stimulus and you think you see a kind of negative of this stimulus for a short time. Accordingly, you can easily create an afterimage yourself by following this description: Provide a black piece of cardboard with a small hole, through which you then fix the bright spot of a light source for a short time. Immediately afterwards, direct your gaze to surfaces at different distances from you (a sheet of paper at arm’s length in front of your face, the wall of your room, or the surface of your desk, etc.). You will perceive an afterimage of the bright hole whose size varies with the distance of the surface. It will appear smaller on paper than on the room’s more distant wall.

Emil Emmert experimented with afterimages as early as 1881 and was the first to recognize the connection between the size of the afterimage and the perceived distance. After him, this consideration of distance has become known as Emmert’s Law. It states that the perceived size of an object G is proportional to the product of distance e and visual angle w (formula 1):

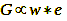
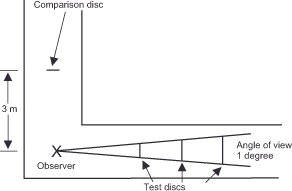
We can prove that this correlation is true through a variety of experiments and correlations. In the test set-up according to Holway and Boring, test persons sit at the intersection of two corridors. They are presented with a test circle disc in one corridor at distances between three and 36 meters and a comparison circle disc in the other corridor at a fixed distance of three meters (figure 65). The subjects are asked to adjust the size of the comparison disk to the test disk after each change in distance. It is crucial that the size of the test disk is increased with increasing distance to ensure that it is always perceived at the visual angle of one degree. The sum of the experiments shows that the subjects adapt the size of the comparison disk almost perfectly to the different physical sizes of the comparison disks. If they see a large but distant test target, they expand the comparison target accordingly. Conversely, when presented with a small test disc at a short distance, they shrink the size of the comparison disc. This adaptation to the actual physical size is remarkable because the test discs always have the same visual angle and, for this reason, always produce retinal images of the same size and supports Emmert’s law: The product of a variable distance and a constant angle of vision is a variable perceived quantity. The reverse case also proves the correlation. If the psychologists take away the depth and distance criteria from the observers by presenting them the test circle disk only through a pinhole and in a corridor covered with dark cloth against the reflections, they lose the ability to adjust the size and see the test disks always in the same size. This is in line with the law governing the angle of vision. And this is also entirely in accordance with Emmert’s law, because the product of a constant angle of vision and an indefinite distance is a constant perceived size. We also perceive the sun and the moon as being of the same size, although their size ratios differ greatly, because we perceive them at the same viewing angle and the space between them does not provide us with any further depth information.

The size of an object is a key criterion for recognizing our surroundings, yet our visual system does not always direct us effectively.

We also find the connection between size and perceived distance in the frequently discussed
moon illusion. Have you ever noticed that the moon appears much larger when it has just risen above the horizon than when it is high in the night sky, even though it is 6,400 kilometers farther away from us near the horizon than at its highest point in the sky? And have you ever wondered how this can be, since it is of fixed size and moves on a relatively stable orbit (the deviation is a maximum of 13%) around our Earth? – While the naked eye can perceive the moon’s different sizes on its slightly elliptical orbit around the earth, the previously described effect is incomparably stronger. In addition, a photo series of the moon, taken with a fixed focal length at intervals of, for example, one hour each, shows our satellite in always the same size. Emmert’s law also applies here, but this time the apparent distance plays the main role. To the question, which part of the sky is farther away, the zenith above the head or the horizon, most people answer with the horizon.
If we put this large apparent distance and the always constant viewing angle of the moon lying in infinity into the formula, its perceived size also increases. The same is true, of course, for the sun, which is close to the horizon and high in the sky. Again, you can provide evidence for the relevance of distance yourself: Look at the moon standing just above the horizon once through a pinhole. This way you turn off the depth and distance information and La Luna shrinks to the same size as at zenith.

The ponzo illusion (or railroad track illusion) belongs to this same category. The two horizontal bars in figure 66 are of the same length and have the same angle of view. Nevertheless, the upper one seems to us to be clearly longer, because the converging railroad tracks simulate spatial depth to us and therefore, with the same angle of vision, we again put a greater distance into the calculation formula and get as a product a perception that is actually too great.

Next

Main Image creation, Depth and Size

Previous Building blocks of our size perception – The angle of vision