Brief attempt about chaos and beauty – Complex systems

You are in „Things and Concepts“

„Why does the silhouette of a storm-bent tree against the evening winter sky strike us as beautiful, but the corresponding outline of a multipurpose building does not, even though the architect has made every effort? The answer seems to me to follow, although this is a bit speculative, from the insights of dynamical systems. Our sense of beauty is inspired by the harmonious arrangement of order and disorder found in natural objects – clouds, trees, mountain ranges, or snow crystals. All these forms are dynamic processes cast into physical shapes, and special combinations of order and disorder are typical of them.“
Physicist Gert Eilenberger in James Gleick, Chaos – Making a new science

Originally, the word chaos comes from Greek mythology and meant the yawning maw leading to the underworld. But already in antiquity, Platon reinterpreted the term to refer to the initial emptiness of the universe before the things within it became existent. Chaos was therefore the unformed original substance. In today’s linguistic usage, chaos carries a negative connotation akin to „mess“ or „disorder“.

Chaos research is dedicated to the study of nonlinear dynamical systems. This sounds cumbersome. However, it pertains to the behavior of systems that follow set rules yet remain impervious to long-term prediction as they respond to even minor changes in initial conditions, leading to significantly altered outcomes. Examples of such systems include the weather, the human heart, the toss of a coin (heads or tails), currents in rivers and the oceans, the shape of blood vessels, growth in general, turbulence in air and water, erosion processes, or the prediction of biological populations.

The first scientist who can rightfully be considered a chaos scientist was Edward Lorenz. Born in Connecticut in 1917, he studied mathematics and meteorology at Dartmouth College, Harvard University, and the Massachusetts Institute of Technology. Before coming to MIT in 1946, where he was a professor of meteorology from 1962 to 1987, he worked in the U.S. Army Weather Service.

1961 was the decisive year. Lorenz had been working on the problem of long-term weather forecasts for a while and had set up a computer program for this purpose that simulated weather patterns on the basis of 12 simple equations. On a winter’s day, he wanted to analyze a particular sequence of the simulation curve again in detail. To avoid having to run the program again from the beginning, he took a shortcut and entered the values from the middle of the curve by hand. Then he started the program and left the computer to its own devices. When he returned from drinking coffee an hour later to pick up the result, he was in for a surprise. Since the values and program were the same, the second run should have produced the same curve. Instead, the printout presented Lorenz with a weather pattern that at first differed only slightly, then sharply, and after only a few months was fundamentally different from the first simulation. Naturally, his initial explanation was a hardware error. At the time, the commonly used vacuum tubes were quite fragile and required frequent replacement. After eliminating this factor, he shifted his focus to data entry. And that’s when the scales fell from his eyes. The program stored the data values with six decimal places. However, in order to conserve paper, the program only printed out three digits. Since the technology of the time was not capable of measuring more precisely than 1/1000 anyway, this accuracy was generally considered to be completely sufficient. Consequently, no one thought it possible that a numerical error in the underlying range could influence the outcome of a calculation. Edward Lorenz’s computer run result demonstrated the untenability of this idea. At the same time, it was clear from that moment on that a serious long-term weather forecast was impossible.

With this, Edward Lorenz had planted the seed for a new science. What he had found later became known as the butterfly effect. Because the difference in the starting point of the two Lorenz curves is so small that one may compare it with the wing beat of this small insect. Probably for this reason, Lorenz titled that 1972 lecture he gave to the American Association for the Advancement of Science, „Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?„

After this insight, Lorenz turned away from weather and looked for a simpler system that also had a sensitive dependence on initial conditions. His computer-based weather system consisted of 12 equations. Now, he aimed to create a system that exhibited the same complex behavior, but with fewer attributes. To that end, he took equations for convection (the rising of hot gas or liquid) and broke them down as much as he could. After that, the equations were no longer related to convection, but the system represented by the three remaining equations continued to exhibit the desired dependence on the primary values. Moreover, they suggested a completely random behavior.

However, when Lorenz plotted the computational results graphically, he obtained a result that completely contradicted the two states of order known at the time. The first described a regular behavior in which the variables never changed. The second denoted a periodic system that moved in a loop, repeating itself infinitely. Lorenz’s equations showed order in any case, for the values were all on a single curve describing a double spiral. However, they never fell on a single point. But since the spiral paths never crossed each other either, the system did not repeat, so it did not show periodic behavior.

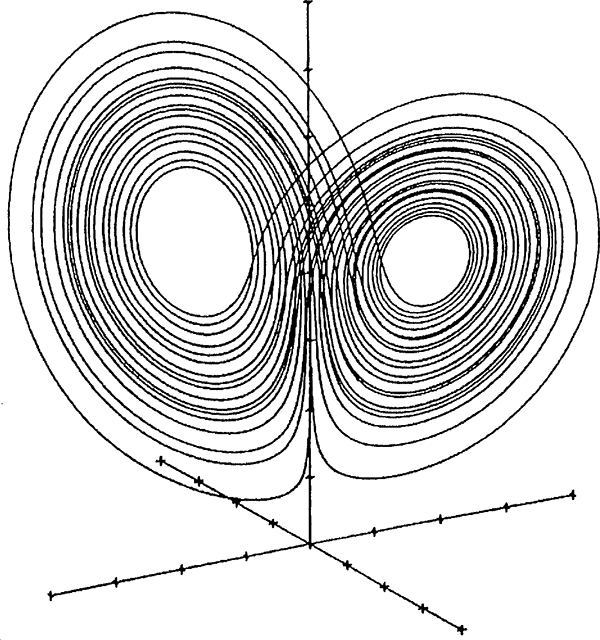
Not order, but also not disorder. The double spiral, which became known as the Lorenz attractor (see figure) and resembles the eye mask of an eagle owl, signals to us a completely new, previously unknown form of order. With it, Edward Lorenz had found order, structure and system in 1963, where previously only chaotic confusion was to be suspected. However, it was to take quite a while before his revolutionary findings fell on fertile ground in the scientific community.

Next Self-similarity

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!