The Logarithm

You are here: Nature Science Photography – Contrast – Basics

Before we delve into the content, I would like to provide a brief explanation of a term that may not be immediately apparent to everyone, yet it permeates the entire material: the logarithm. The logarithm stems from ancient Greek λόγος lógos „understanding, teaching, ratio“ as well as ancient Greek
αριθμός arithmós „number“. The logarithm is thus a „ratio“. It belongs to the elementary mathematical functions.

…in mathematics

The formula symbol for the logarithm is log. The base is added as an index. Rarely one finds also from it deviating spellings, as, for example, _bloga, or the basis is not noted, if it is evident from the context and no danger of confusion exists. One writes:

Formula 1

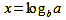
and says: „x is the logarithm of a to the base b“ or also „x is the logarithm to the base b from a“. a is called numerus. The logarithmization result reveals the exponent x needed to exponentiate the base b to obtain the logarithm (numerus) a. Formally, logarithms are all solutions of the equation

Formula 2

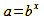
to given quantities a and b.

Depending on the number range and for which quantities this equation is considered, it has no, several, or exactly one solution. For example, 3 is the (real) logarithm of 8 to the base 2, written log₂8 = 3, because it is 2³ = 8. If the above equation is to be solved to b instead of x, the solution is given by the x-th root of a. The following types and notations of the logarithm occur:

log_b Logarithm to base b

In logarithmus naturalis, or natural logarithm, the logarithm to base e, Euler’s number 2.7182818284590452…

lg The logarithm decadic, also known as the logarithm of ten or Briggs logarithm, represents the logarithm to base 10. It is useful because of the decimal system and is used by many calculators

ld logarithmus dualis, logarithm to base 2, also called the two logarithm or dyadic or binary logarithm (sometimes abbreviated); used in computer science because of the binary system

log When the context clearly indicates it or a convention specifies it, we use the symbol log without a specified base. In technical applications (e.g., on most pocket calculators), log usually stands for the decadic logarithm; in computer science for the dyadic logarithm. Mathematicians and physicists usually use log for the natural logarithm. Occasionally, mathematicians and physicists also use log when the base is not significant.

…in photography

In photography, we encounter logarithmic relationships everywhere. The f-stops on lenses, the exposure times on cameras, or the sensitivity values of films or electronic image carriers are all based on a logarithmic system. A change of a whole f-stop on a lens or a whole time step on a camera allows twice or half the amount of light to reach the photolayer. Changing the DIN value of a film by 3 DIN, or its ASA number by a factor of 2, also leads to a doubling or halving of the effective amount of light. This has to do with the fact that the logarithmic expression reflects a fundamental property of our visual perception. This, like many other perceptions, is not linear but rather logarithmic in nature. This is exceedingly helpful in covering a wide range of intensities with limited perceptual ability. That is, we perceive one stimulus as stronger compared to another only if it differs from it by a certain factor. If our perceptual apparatus operated in many areas not logarithmically but linearly, we would, for instance, perceive a doubling of intensity as twice as bright, potentially leading to permanent blindness in the presence of abundant light on a sunny day. The comparison between a linear and a logarithmic scale reveals what this means. The significance of the logarithm is probably clearest here.

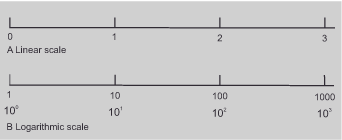
The upper scale in figure 5 A is constructed as an arithmetic series, i.e., each step is equidistant from the next. Here, one is always added from one step to the next. This is a linear progression. The lower scale in figure 5 B is built up as a geometric series, i.e., each step is distant from the next by the same factor. Here the markings differ by a multiplicative factor of 10. This is a logarithmic progression. Therefore, the second step represents a value ten times greater than the first, the third step represents a value ten times greater than the second, and so on. We express these values as powers of ten, signifying equal steps in power between 10¹ and 10³. The logarithm is a means of expressing these values. The logarithm of a number y, described as log_y, is defined as follows:

Formula 4

The logarithm of the markings in figure 5 B is therefore log 10 = 1, because 10¹ = 10, log 100 = 2, because 10² = 100, and so on. Thus the markings correspond to equal steps on a logarithmic scale. Practically, such ways of representation are always used when it is necessary to present wide gradations clearly.

When describing photographic materials, we usually deal with logarithms on base 10. The conversion of log10 units into exposure steps goes like this: One exposure step means the doubling or halving of the amount of light and the Logarithm of ten of 2 = 0.3 (10^0.3=2). So, assuming a dynamic range of 3.3 log₁₀ units, 3.3/0.3 = 11 exposure steps.

Next The characteristic curve

Main Contrast

Previous What contrast is and how to determine it

If you found this post useful and want to support the continuation of my writing without intrusive advertising, please consider supporting. Your assistance goes towards helping make the content on this website even better. If you’d like to make a one-time ‘tip’ and buy me a coffee, I have a Ko-Fi page. Your support means a lot. Thank you!